You are given a set of n disks in the plane. The disks can have different radii. No two disks intersect or touch each other.

Your job is to draw n-1 straight line segments to connect the disks, such that there exists a path from any disk to any other disk, that only walks on the circumference or inside the areas of any of the n disks, or on the line segments.

There are some constraints on the line segments:

• The line segments should have integer coordinate endpoints in the range [0, 10^9].
• A line segment can only touch or intersect with at most two disks.
• Any two line segments cannot intersect, and cannot touch. The only exception is that it is allowed for two line segments to share an endpoint.

Input Format

The first line contains an integer n, denoting the number of disks.

Each of the next n lines contains the description of a disk. Each line contains three integers x[i], y[i] and r[i], denoting a disk with centre point (x[i], y[i]) and a radius of r[i].

Constraints

• 2 ≤ n ≤ 2 × 10^5
• 0 ≤ x[i], y[i] ≤ 10^9
• 1 ≤ r[i] ≤ 10^9
• It is guaranteed that no two disks touch or intersect.

Output Format

Output YES if there exists a solution, otherwise print NO. If the answer is YES, on the following lines output a description of the line segments.

The description contains n-1 lines. Each of the n-1 lines should contain 4 integers x[1], y[1], x[2], y[2], denoting a line segment that connects the points (x[1],y[1]) and (x[2],y[2]). These two points should not be the same. Further more it must hold that 0 ≤ x[1], y[1], x[2], y[2] ≤ 10^9. It can be proven that if the answer is YES, then there exists a solution in which the coordinates of the line segments are bounded like this.

Sample 1

Input

3
1 0 3
10 10 6
0 5 1

Output

YES
0 4 7 12
0 0 16 8

Sample 2

Input

2
1 1 1
3 3 1

Output

YES
2 1 3 2

Sample 3

Input

5
10 10 10
2 0 1
20 20 1
3 20 1
20 0 1

Output

YES
1 0 10 10
20 0 10 10
20 10 20 22
3 20 10 10

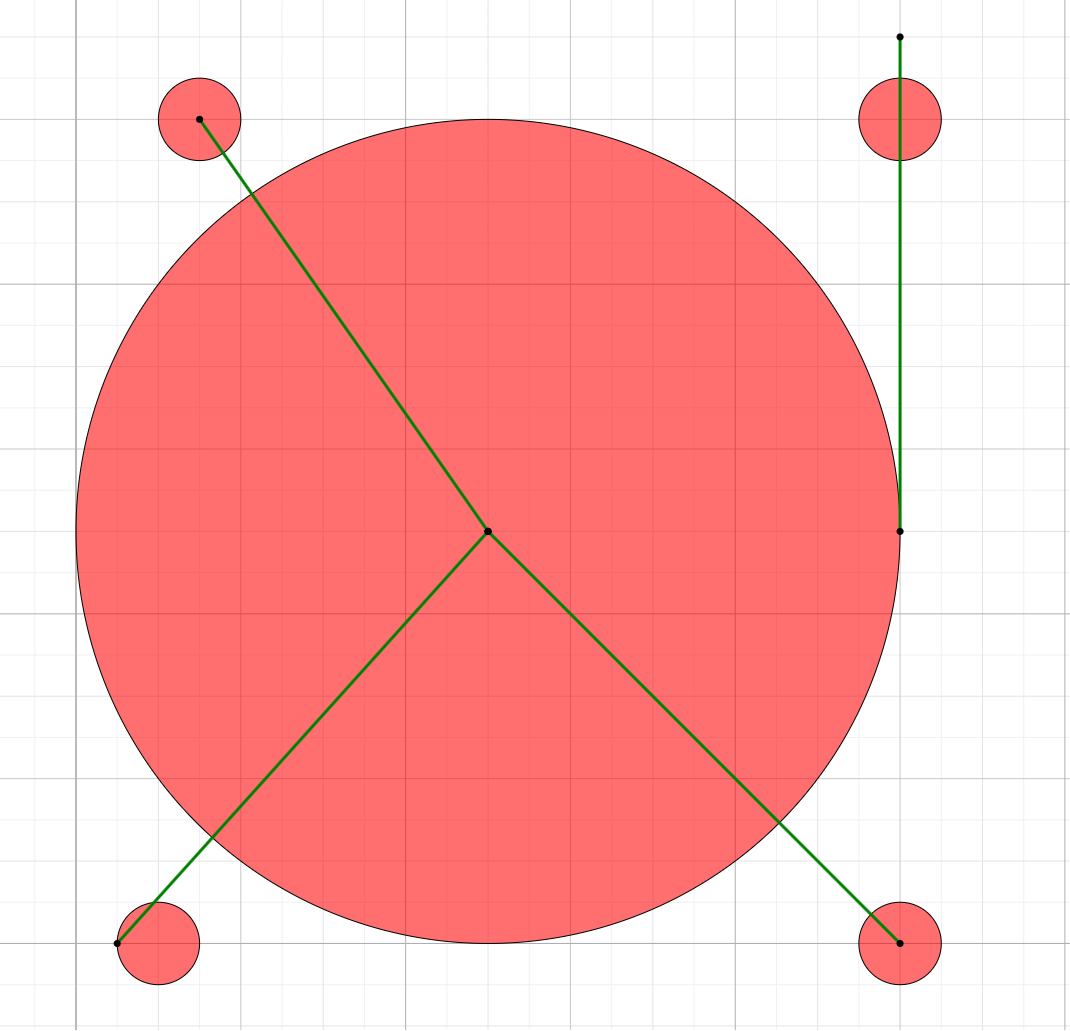
Visualisation of sample 3